In den vergangenen Monaten habe ich mich in den STM32F4-Controller eingearbeitet, um ein (Roboter-)Projekt damit umzusetzen. Genauer gesagt, handelt es sich um einen Roboter, der über Mecanum-Räder (oder auch swedish-wheels) verfügt. Diese Räder zeichnen sich deshalb besonders aus, weil auf dem Außenring der Felge, Gummiwalzen im 45° Winkel angeordnet sind, welche sich passiv über den Untergrund abrollen. Dadurch verfügt der Roboter über einen weiteren Freiheitsgrad. Das bedeutet, dass der Roboter – trotz fehlender Lenkachse – alle Richtungen (X, Y und Θ) auf der Ebene erreichen kann und deshalb die maximale Bewegungsfreiheit hat. X und Y entspricht dabei Bewegungen in die die entsprechenden Richtungen und Θ bezeichnet die Drehbewegung des Roboters.
Der Roboter
Bei dem Roboter handelt es sich um den Nexus 4WD. Dieser verfügt über vier Faulhaber Motoren, welche direkt mit Inkrementalgebern ausgestattet sind, (Ultraschall-)Distanzsensoren und einem Arduino Controller, auf dem auch direkt passende Motortreiber vorhanden sind. Die 12 V Gleichstrommotoren, wie aus die restliche Hardware werden über einen Akku versorgt, der mit einem gewöhnlichen Tamiya Stecker angeschlossen wird.
Da ich mich für den STM32F4 entschieden habe, wurden einige Modifikationen an dem Roboter durchgeführt. Insbesondere der Arduino-Controller wurde durch den STM32F4 ausgetauscht, was aber zur Folge hatte, dass die Motortreiber, welche fest auf der Platine des Arduinos verbaut waren, ebenfalls aus dem Roboter entfernt wurden. Deshalb musste eine neue Motorsteuerung mit entsprechenden Treiber (H-Brücken) entwickelt werden, damit die Motoren richtig angesteuert werden können. Zusätzlich zu den vorhandenen Sensoren und Aktoren, wurde der Roboter mit einem Gyroskop ausgestattet, damit die Orientierung, also die Drehbewegungen des Roboters, im Rahmen der Odometrie gemessen werden kann.
Die Abbildung1 und Abbildung2 zeigen den Roboter mit geöffnetem Chassis. Man kann die vier Mecanum-Räder erkennen, welche an den Wellen der Motoren befestigt sind. Außerdem sieht man – trotz der vielen Leitungen – die Hardwarekomponenten und den Akku. Abbildung2 stellt den Roboter noch einmal in der Vogelperspektive dar und Abbildung3 hebt die individuell nachgerüstete Hardware besonders hervor.
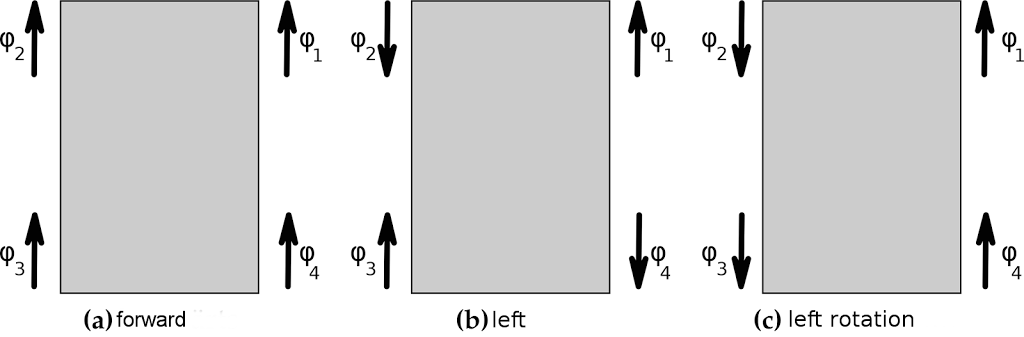
Die Bewegungsrichtung des omnidirektionalen Roboters ist davon abhängig, wie die Räder angeordnet sind und wie diese sich drehen. Bei diesem Roboter sind die Mecanumräder so angeordnet, dass die Walzen bei der Sicht von oben, in die Fahrzeugmitte zeigen. Dadurch sind die Bewegungsrichtungen fest durch die Radbewegungen definiert. Abbildung4 zeigt drei Szenarien, die verdeutlichen sollen, wie sich die Drehrichtungen der Räder auf die Bewegung des Roboters auswirken. So sieht man in Beispiel (a), dass alle Räder sich nach vorne drehen. Die resultierende Bewegung des Roboters ist somit eine Vorwärtsbewegung. In Beispiel (b) drehen sich die Räder in unterschiedliche Richtungen. Die auf der linken Seite des Roboters drehen sich nach Innen, während die Räder auf der Rechten Seite sich nach außen drehen. Die resultierende Bewegung ist eine Bewegung in Richtung Y auf der Ebene. Bei dem dritten Beispiel drehen sich die Räder der linken Seite nach hinten, während die auf der rechten Seite sich nach vorne drehen. Daraus resultiert eine Linksdrehung des Roboters.
Motorsteuerung
Die Motortreiber des Roboters wurden wie oben bereits erwähnt, mit dem Arduino aus dem Roboter entfernt. Deshalb wurde eine Platine entwickelt, auf der sich zwei Motortreiber vom Typ TB6612FNG von Toshiba befinden. Die Treiber können jeweils zwei Motoren steuern, deshalb wurden insgesamt zwei Stück eingesetzt. Diese Motortreiber sind ein wenig unterdimensioniert, denn die Motoren sind im Datenblatt mit einem maximalen Strom von 1,4A angegeben. Da die Motortreiber allerdings nur einen maximalen Strom von 1,2A aushalten, wurde die Motorleistung in der Software auf maximal 80% begrenzt. In der Software wird (durch den STM32F4) ein PWM-Signal generiert, durch das die Treiber eine entsprechende Spannung an die Motoren anlegen. Dadurch kann die Leistung der Motoren beeinflusst werden.
Inkrementalgeber
Inkrementalgeber sind Sensoren, die eine Rotation messen. Damit kann die Winkelgeschwindigkeit einer Rotation mit Hilfe einer Zeitmessung bestimmt werden. Durch Integration kann aus dieser Winkelgeschwindigkeit, der zurückgelegte Winkel ermittelt werden. Da der Durchmesser bzw. der Radius der Räder fix ist, dann durch eine Multiplikation des Winkels mit dem Radradius, die zurückgelegte Distanz berechnet werden.
Der Nexus-Roboter verfügt über photoelektrische Inkrementalgeber, welche insgesamt 12 Impulse pro Umdrehung generieren. Photoelektrische Inkrementalgeber emittieren ein Lichtimpuls durch eine rotierende Messscheibe. Dadurch werden periodische Signale generiert, die einen Schluss auf die Geschwindigkeit und Richtung des Rades ermöglichen. Dieses Signal wird von den Encodern des STM32F4-Controller ausgewertet und in der Software verarbeitet. Die Motoren sind mit einem Getriebe im Verhältnis 64:1 übersetzt. Dadurch erhöht sich die Anzahl der Impulse um den Faktor 64 auf insgesamt 768 Schritte pro Umdrehung. Durch eine sogenannte Vierfachauswertung, werden die Impulse noch einmal um den Faktor vier, auf insgesamt 3072 Impulse pro Umdrehung, erhöht. Daraus ergibt sich eine Auflösung der Inkrementalgeber von ungefähr 0,117°.
Das folgende Beispiel zeigt die Initialisierung eines Encoders mit Vierfachauswertung:
void initEncoders(fahrzeug_t *fz) {
fz->encoder[0].id = ENCODER_1;
fz->encoder[0].direction = FORWARD;
GPIO_InitTypeDef GPIO_InitStructure;
// Takt fuer die Ports einschalten
RCC_AHB1PeriphClockCmd(ENC1A_GPIO_CLK, ENABLE);
RCC_AHB1PeriphClockCmd(ENC1B_GPIO_CLK, ENABLE);
GPIO_StructInit(&GPIO_InitStructure);
GPIO_InitStructure.GPIO_Mode = GPIO_Mode_AF;
GPIO_InitStructure.GPIO_PuPd = GPIO_PuPd_UP;
/************************* MOTOR1 *************************************/
GPIO_InitStructure.GPIO_Pin = ENC1A_PIN;
GPIO_InitStructure.GPIO_Speed = GPIO_Speed_100MHz;
GPIO_Init(ENC1A_GPIO_PORT, &GPIO_InitStructure);
GPIO_InitStructure.GPIO_Pin = ENC1B_PIN;
GPIO_Init(ENC1B_GPIO_PORT, &GPIO_InitStructure);
GPIO_PinAFConfig(ENC1A_GPIO_PORT, ENC1A_SOURCE, ENC1A_AF);
GPIO_PinAFConfig(ENC1B_GPIO_PORT, ENC1B_SOURCE, ENC1B_AF);
RCC_APB1PeriphClockCmd(ENC1_TIMER_CLK, ENABLE);
// Vierfachauswertung
TIM_EncoderInterfaceConfig(ENC1_TIMER, TIM_EncoderMode_TI12,
TIM_ICPolarity_Rising, TIM_ICPolarity_Rising);
TIM_SetAutoreload(ENC1_TIMER, 0xffff);
TIM_Cmd(ENC1_TIMER, ENABLE);
}Die gezählten Impulse können anschließend über den Timer ausgelesen werden:
int32_t getEncoderValue(encoder_t *enc) { switch (enc->id) {
case ENCODER_1:
enc->currentValue = TIM_GetCounter(ENC1_TIMER);
TIM_SetCounter(ENC1_TIMER, 0);
break;
case ENCODER_2:
enc->currentValue = TIM_GetCounter(ENC2_TIMER);
TIM_SetCounter(ENC2_TIMER, 0);
break;
case ENCODER_3:
enc->currentValue = TIM_GetCounter(ENC3_TIMER);
TIM_SetCounter(ENC3_TIMER, 0);
break;
case ENCODER_4:
enc->currentValue = TIM_GetCounter(ENC4_TIMER);
TIM_SetCounter(ENC4_TIMER, 0);
break;
}
return enc->currentValue;
}Gyroskop
Das Gyroskop wird dazu eingesetzt, die relative Winkeländerung des Roboters zu messen. Auf dem Roboter wurde ein GyroClick-Modul der Firma MikroElektronika verbaut, welches mit dem L3GD20-Drehratensensor ausgestattet ist (siehe Abbildung5). Da der Roboter holonomen Zwangsbedingungen unterliegt (dieser sich nur auf der Ebene bewegen kann), ist die Auswertung der Gierrate ausreichend. Es werden also nur Drehungen um die Z-Achse ausgewertet, weil diese relativen Orientierung des Roboter entsprechen. Das Gyroskop misst die Geschwindigkeiten einer Drehung, welche durch Integration über die Zeit auf den relativen Winkel schließen lässt. Für die Kommunikation mit dem STM32F4 wurde ein SPI Bus eingesetzt und so konfiguriert, dass das Gyroskop mit einer Abtastrate von 760Hz ausgelesen wird.

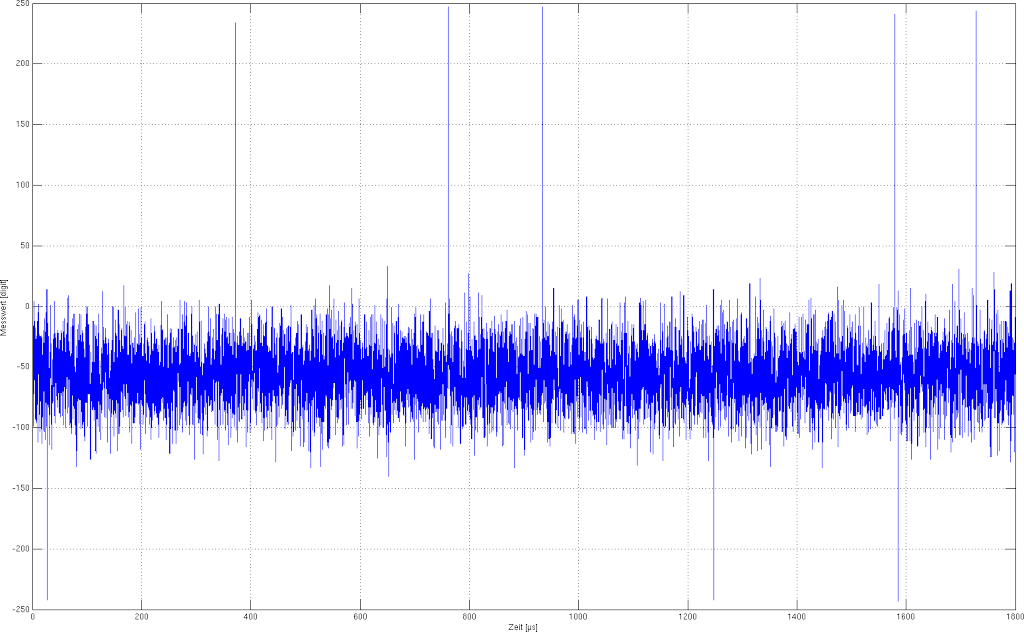
Da das Gyroskop driftet, wurde eine Kalibrierung in zwei Schritten durchgeführt. Als erstes wurde der Bias durch mehrere Referenzmessungen in der Nulllage, während der Initialisierungsphase, durch das arithmetische Mittel (Mittelwert) bestimmt. Dieser kann bei den Messungen als Offset aus dem Ergebnis rausgerechnet werden. Abbildung6 zeigt eine aufgezeichnete Referenzmessung, aus der ersichtlich ist, wie die Messwerte des Gyroskopes in der Nullage verschoben sind (Offset). Bei dieser Messung lag der Bias bei ungefähr -56, was bei der (Gyro-)Auflösung von 8,75 °/s, einem Offset von ca. -0,49 °/s entspricht.
Die zweite Methode zur Unterdrückung des Driftverhalten ist der Einsatz einer Schranke. In der Software wurde eine Untergrenze definiert, welche die minimale Winkelgeschwindigkeit beschreibt, die gemessen werden muss, damit die Software diese Winkeländerung aus auswertet. Dadurch können sehr kleine Winkeländerungen zwar nicht mehr genau gemessen werden, jedoch reduziert sich das Driftverhalten erheblich, sodass diese in Kauf genommen wurde.
Das Gyroskop misst die Winkeländerungen pro Zeit. Um den relativen Winkel der Drehbewegung zu erhalten, wird die gemessene Winkeländerung über die Zeit integriert. In der Software wurde für die Implementierung das Trapezverfahren eingesetzt. Die Berechnung des Offsets wird mit Hilfe des arithmetischen Mittels von 2000 Messungen durchgeführt:
void calcGyroOffsetSpi(void) {
int32_t data = 0;
for (int i = 0; i < 2000; i++) {
data += readGyroscopeZAxis();
}
spiGyroOffset = (data / 2000);
}Für das Rauschen wird eine Grenze definiert, welche die gemessene Winkelgeschwindigkeit überschreiten muss, damit diese als Winkeländerung detektiert wird. Die Berechnung dieser Grenze wird wie folgt durchgeführt:
void calcGyroNoiseSpi(void){
int32_t ZG = 0;
for(int i=0;i<2000;i++){
ZG = readGyroscopeZAxis();
if(ZG-spiGyroOffset > spiGyroNoise){
spiGyroNoise = (int) ZG-spiGyroOffset;
}else if((int)ZG-spiGyroOffset < -spiGyroNoise){
spiGyroNoise = -((int) ZG-spiGyroOffset);
}
}
spiGyroNoise = spiGyroNoise / 114;
}
Mit diesen Werten kann nun der relative Winkel durch Integration mit dem Trapezverfahren ermittelt werden. Der Winkel ist auf das Intervall [0°,360°] abgebildet:
gyro_t* calcSpiGyroDelta(uint32_t delta) {
lastValue = value;
int16_t val = readGyroscopeZAxis();
gyroData->angleDelta = 0.0;
value = ((double) (val - spiGyroOffset) / 114); // 1 / (8.75 * 10^-3) [1/mdps] = 114.29 [s/d]
if(value >= spiGyroNoise || value <= -spiGyroNoise){
gyroData->angleDelta = ((double) ((value + lastValue)) * delta / (2000000));
gyroData->angle += gyroData->angleDelta;
}
if (angle < 0) {
gyroData->angle += 360;
} else if (angle >= 360) {
gyroData->angle -= 360;
}
return gyroData;
}
Odometrie
Odometrie ist ein Verfahren, mit dem die relative Position von bodengebundenen Fahrzeugen, durch die Bewegung der Räder (oder Schritte bei humanoiden Roboter) bestimmt werden kann. Da viele Roboter über die Möglichkeit verfügen, Radbewegungen zu messen, wird die Odometrie besonders gerne zur Lokalisierung eingesetzt, weil die notwendige Sensorik schon im Rahmen von anderen Anforderungen vorhanden ist. Das Verfahren basiert dabei auf der Tatsache, dass die Drehungen der Räder auf Distanzen umgerechnet und aufsummiert werden. Dadurch kann die Bewegung des Roboters nachvollzogen werden.
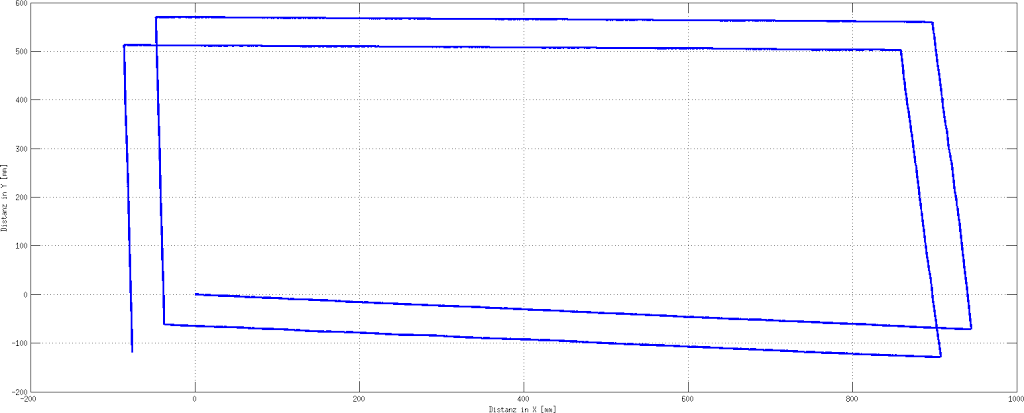
Da die Abtastrate in der Software bei 5ms liegt werden viele Daten im Rahmen der Odometrie generiert. Diese werden mit Hilfe eines DMA-Bausteins und der Bibliothek FatFs per SPI auf einer microSD-Karte gespeichert und stehen einer späteren Auswertung somit zur Verfügung. Abbildung7 zeigt die aufgezeichneten Odometriedaten einer Testfahrt des Roboters.
Die Messung wurde über eine Distanz von 6280mm durchgeführt und der Roboter dabei kontinuierlich lokalisiert. Man sieht, dass der Roboter einen Versatz bei der Geradeausfahrt hat. Dies ist darauf zurückzuführen, dass bisher keine Drehzahlregelung implementiert wurde.